неділя, 1 квітня 2018 р.
Математичний дивертисмент.
(Помістити один мішок в інший)
Дві бабці вирушили з Києва у Вінницю.
Обидві вони пройшли 200 верств.
Скільки верств пройшла кожна з них,
якщо йшли вони з однаковою швидкістю?
(Кожна пройшла 200 верств)
Скільки кінців у чотирьох кілочків?
У п’яти кілочків? А у п’яти з половиною?
(8, 10, 12)
Як від двадцяти відняти 88 так,
щоб залишилось 22?
(ХХ-88=22)
Які числа більші сто при читанні
не змінюються від їх перевертання?
(609, 888, 6969, 69869, …)
Число 66 вмить збільшіть на половину цього числа.
(Перевернути число, отримаємо 99)
Число 666 вмить збільшіть у півтори рази.
(Перевернути число, отримаємо 999)
Розділіть число 188 на дві рівні частини,
щоб у кожній з них отримали сто.
(188)
Розділіть на аркуші паперу число дванадцять
на дві рівні частини так, щоб половина цього числа була сім.
Скільки кінців у п’яти кілочків?
А у п’яти з половиною?
А у шести з четвертиною?
(10, 12, 14)
Учні розпилюють колоду на метрові куски
Відпилювання займає одну хвилину.
За скільки хвилин вони розпиляють колоду довжиною 5 метрів?
(за 4 хвилини)
На поляні поблизу болота паслися
протягом однієї години двоє однакових
коней з однаковим апетитом.
Відрізнялися вони один від одного лише тим,
що у одного коня хвіст був вдвічі коротший,
ніж у другого? Який з коней зів більше трави,
якщо вони розпочали і закінчили пастися одночасно?
(Кінь з довшим хвостом зїв більше,
Один чоловік купив три кози і заплатив 300 гривень.
Запитується: по чому пішла кожна коза?
(По землі)
Мельник зайшов у млин. В кожному з чотирьох кутків
він побачив по три мішки, на кожному мішку сиділо по
три кішки, а кожна кішка мала при собі трьох кошенят.
Запитується, чи багато ніг було у млині?
(Жодної, у кішок лапи)
Що це може бути: дві голови,
дві руки і шість ніг, а в ходьбі лише чотири?
(Вершник на коні)
Розділіть число 1888 на дві рівні частини,
щоб у кожній з них отримали тисячу.
(1888)
На лісопильному заводі машина відпилює кожної
хвилини від колоди кусок довжиною в одну десяту аршина.
За скільки хвилин така машина розпиляє колоду довжиною в 1 аршин?
(9 хвилин)
Зобразіть число від 1 до 31 тільки шістьма трійками та математичними діями:
(3*3*3+3+3:3; 33-3+3:3; 33-(3+3):3)
Як можна 40 гривень (сорок монет номіналом по 1 гривні)
помістити в великий та маленький гаманці, щоб
в маленькому гаманці лежала одна частина грошей,
а у великому гаманці було аж сорок частин грошей?
( покласти в маленький гаманець 1 гривню і закрити його,
потім засунути цей маленький гаманець у великий гаманець і
покласти у великий гаманець ще 39 грн)
Два батьки і два сини з’їли
за сніданком троє яєць,
причому кожному з них дісталося
по цілому яйцю. Як це могло статися?
(Це було троє осіб: дід, батько і син)
помістити в великий та маленький гаманці, щоб
в маленькому гаманці лежала одна частина грошей,
а у великому гаманці було аж сорок частин грошей?
( покласти в маленький гаманець 1 гривню і закрити його,
потім засунути цей маленький гаманець у великий гаманець і
покласти у великий гаманець ще 39 грн)
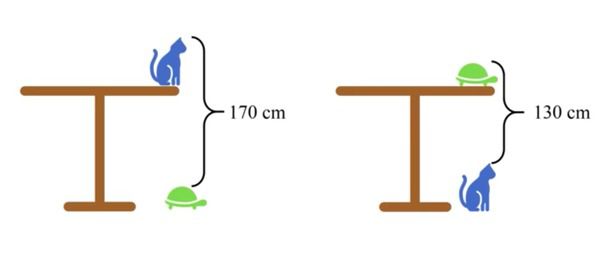
Китайська логічна задачка з математики
Яка змусила багатьох користувачів в Інтернеті міцно задуматися.
Знайти висоту стола. На скільки кіт вищий, ніж черепаха?
Два батьки і два сини з’їли
за сніданком троє яєць,
причому кожному з них дісталося
по цілому яйцю. Як це могло статися?
(Це було троє осіб: дід, батько і син)
Дві бабці вирушили з Києва у Вінницю.
Обидві вони пройшли 200 верств.
Скільки верств пройшла кожна з них,
якщо йшли вони з однаковою швидкістю?
(Кожна пройшла 200 верств)
Скільки кінців у чотирьох кілочків?
У п’яти кілочків? А у п’яти з половиною?
(8, 10, 12)
Як від двадцяти відняти 88 так,
щоб залишилось 22?
(ХХ-88=22)
Які числа більші сто при читанні
не змінюються від їх перевертання?
(609, 888, 6969, 69869, …)
Число 66 вмить збільшіть на половину цього числа.
(Перевернути число, отримаємо 99)
Число 666 вмить збільшіть у півтори рази.
(Перевернути число, отримаємо 999)
Розділіть число 188 на дві рівні частини,
щоб у кожній з них отримали сто.
(
Розділіть на аркуші паперу число дванадцять
на дві рівні частини так, щоб половина цього числа була сім.
Скільки кінців у п’яти кілочків?
А у п’яти з половиною?
А у шести з четвертиною?
(10, 12, 14)
Учні розпилюють колоду на метрові куски
Відпилювання займає одну хвилину.
За скільки хвилин вони розпиляють колоду довжиною 5 метрів?
(за 4 хвилини)
На поляні поблизу болота паслися
протягом однієї години двоє однакових
коней з однаковим апетитом.
Відрізнялися вони один від одного лише тим,
що у одного коня хвіст був вдвічі коротший,
ніж у другого? Який з коней зів більше трави,
якщо вони розпочали і закінчили пастися одночасно?
(Кінь з довшим хвостом зїв більше,
так як він мав змогу відганяти мух і оводів,
котрі заважали коням пастися)
Один чоловік купив три кози і заплатив 300 гривень.
Запитується: по чому пішла кожна коза?
(По землі)
Мельник зайшов у млин. В кожному з чотирьох кутків
він побачив по три мішки, на кожному мішку сиділо по
три кішки, а кожна кішка мала при собі трьох кошенят.
Запитується, чи багато ніг було у млині?
(Жодної, у кішок лапи)
Що це може бути: дві голови,
дві руки і шість ніг, а в ходьбі лише чотири?
(Вершник на коні)
Розділіть число 1888 на дві рівні частини,
щоб у кожній з них отримали тисячу.
(
На лісопильному заводі машина відпилює кожної
хвилини від колоди кусок довжиною в одну десяту аршина.
За скільки хвилин така машина розпиляє колоду довжиною в 1 аршин?
(9 хвилин)
Зобразіть число від 1 до 31 тільки шістьма трійками та математичними діями:
(3*3*3+3+3:3; 33-3+3:3; 33-(3+3):3)
Зобразіть число 100 чотирма однаковими цифрами ( від 1 до 9) та арифметичними діями.
пʼятниця, 23 березня 2018 р.
пʼятниця, 23 лютого 2018 р.
Зростаючий порядок цифр
Задача. Зростаючий порядок цифр у натуральному числі
Скільки існує n-цифрових чисел, усі цифри яких записані в строго зростаючому порядку, якщо вважати правильними n-цифрові записи чисел: 000..01 =1, 00..0012=12, 000…000123=123 і так далі
Розв'язання. Зрозуміло, що треба розглядати випадок, коли n<11.
Спочатку знайдемо кількість 10-цифрових чисел, у яких усі цифри різні і розташовані у довільному порядку.
В розряд одиниць такого 10-цифрового числа можна записати 10-ма способами будь-яку цифру, бо різних цифр 10: {0;1;2;3;4;5;6;7;8;9}.
В розряд десятків такого 10-цифрового числа можна записати 9 способами деяку цифру, бо 10-1=9 цифр, так як одна цифра уже стоїть в розряді одиниць, тобто використана.
В розряд сотень такого 10-цифрового числа можна записати 8 способами деяку цифру, бо 10-2=8 цифр, так як дві цифри уже стоять в розряді одиниць та десятків, тобто використані.
Аналогічно міркуємо до розряду одиниць мільярдів, в який можна буде записати лише одним способом цифру. Скористаємося правилом добутку, отримаємо, що існує 10!=1*2*3*4*5*6*7*8*9*10=3628800 чисел, у яких усі цифри різні і розташовані у довільному порядку.
Порахуємо кількість десятицифрових чисел, усі цифри яких записані в строго зростаючому порядку.
З десяти різних цифр можна утворити 3628800 10-цифрових чисел, у яких цифри не повторюються і розташовані в довільному порядку, серед яких лише в одному випадку цифри розташовані в зростаючому порядку. Тому шукані числа становитимуть 1/3628800 всіх 10-цифрових чисел з різними цифрами.
Тепер знайдемо кількість 9-цифрових чисел, у яких усі цифри різні і розташовані у довільному порядку.
В розряд одиниць такого 9-цифрового числа можна записати 10-ма способами будь-яку цифру, бо різних
одна цифра уже стоїть в розряді одиниць, тобто використана.
В розряд сотень такого 9-цифрового числа можна записати 8 способами деяку цифру, бо 10-2=8 цифр, так як дві цифри уже стоять в розряді одиниць та десятків, тобто використані.
Аналогічно міркуємо до розряду сотень мільйонів, в який можна буде записати лише одним способом цифру, бо різних цифр 10: {0;1;2;3;4;5;6;7;8;9}.
В розряд десятків такого 9-цифрового числа можна записати 9 способами деяку цифру, бо 10-1=9 цифр, так як. Скористаємося правилом добутку, отримаємо, що існує 2*3*4*5*6*7*8*9*10=3628800 чисел, у яких усі цифри різні і розташовані у довільному порядку.
Порахуємо кількість дев'ятицифрових чисел, усі цифри яких записані в строго зростаючому порядку.
З десяти різних цифр можна утворити 3628800 9-цифрових чисел, у яких цифри не повторюються і розташовані в довільному порядку. З дев'яти різних цифр утворюємо різні перестановки, серед яких лише в одному випадку цифри розташовані в зростаючому порядку. Тому шукані числа становитимуть 1/9! всіх 9-цифрових чисел з різними цифрами. 3628800/9!=10 чисел, що мають 9 різних цифр і розташовані в зростаючому порядку.
Тепер знайдемо кількість 8-цифрових чисел, у яких усі цифри різні і розташовані у довільному порядку.
В розряд одиниць такого 8-цифрового числа можна записати 10-ма способами будь-яку цифру, бо різних 10 цифр.
В розряд десятків такого 9-цифрового числа можна записати 9 способами деяку цифру, бо 10-1=9 цифр, так як одна цифра уже стоїть в розряді одиниць, тобто використана.
В розряд сотень такого 8-цифрового числа можна записати 8 способами деяку цифру, бо 10-2=8 цифр, так як дві цифри уже стоять в розряді одиниць та десятків, тобто використані.
Аналогічно міркуємо до розряду десятків мільйонів, в який можна буде записати лише одним способом цифру, бо різних цифр 10: {0;1;2;3;4;5;6;7;8;9}.
Скористаємося правилом добутку, отримаємо, що існує 3*4*5*6*7*8*9*10=1814400 чисел, у яких усі цифри різні і розташовані у довільному порядку.
Порахуємо кількість 8-цифрових чисел, усі цифри яких записані в строго зростаючому порядку.
З десяти різних цифр можна утворити 1814400 8-цифрових чисел, у яких цифри не повторюються і розташовані в довільному порядку. З восьми різних цифр утворюємо різні перестановки, серед яких лише в одному випадку цифри розташовані в зростаючому порядку. Тому шукані числа становитимуть 1/8! всіх 9-цифрових чисел з різними цифрами. 1814400/8!=45 чисел, що мають 8 різних цифр і розташовані в зростаючому порядку.
Тепер знайдемо кількість 7-цифрових чисел, у яких усі цифри різні і розташовані у довільному порядку.
В розряд одиниць такого 7-цифрового числа можна записати 10-ма способами будь-яку цифру, бо 10 різних цифр.
В розряд десятків такого 7-цифрового числа можна записати 9 способами деяку цифру, бо 10-1=9 цифр.
В розряд сотень такого 7-цифрового числа можна записати 8 способами деяку цифру, бо 10-2=8 цифр, так як дві цифри уже стоять в розряді одиниць та десятків, тобто використані.
Аналогічно міркуємо до розряду одиниць мільйонів, в який можна буде записати лише одним способом цифру, із різних цифр 10: {0;1;2;3;4;5;6;7;8;9}.
Скористаємося правилом добутку, отримаємо, що існує 4*5*6*7*8*9*10=604800 чисел, у яких усі цифри різні і розташовані у довільному порядку.
Порахуємо кількість 7-цифрових чисел, усі цифри яких записані в строго зростаючому порядку.
З десяти різних цифр можна утворити 604800 7-цифрових чисел, у яких цифри не повторюються і розташовані в довільному порядку. З 7 різних цифр утворюємо різні перестановки, серед яких лише в одному випадку цифри розташовані в зростаючому порядку. Тому шукані числа становитимуть 1/7! всіх 9-цифрових чисел з різними цифрами. 604800/7!=120 чисел, що мають 8 різних цифр і розташовані в зростаючому порядку.
І так далі.
Для 6-цифровиих отримаємо: 151200/6!=210 чисел, у яких цифри розташовані у зростаючому порядку.
Для 5-цифровиих отримаємо: 30240/5!=252 чисел, у яких цифри розташовані у зростаючому порядку.
Для 4-цифровиих отримаємо: 5040/4!=210 чисел, у яких цифри розташовані у зростаючому
Для 3-цифровиих отримаємо: 720/3!=120 чисел, у яких цифри розташовані у зростаючому порядку.
Для 2-цифровиих отримаємо: 90/2!=45 чисел, у яких цифри розташовані у зростаючому порядку.
Для 1-цифровиих отримаємо: 10/1!=10 чисел, у яких цифри розташовані у зростаючому порядку.
Загальна кількість натуральних чисел, у яких цифри розташовані у зростаючому порядку: 2(10+45+120+210)+252 =1022 (враховуючи і одноцифрові натуральні числа та нуль)
середа, 21 лютого 2018 р.
Стратегічна задача на оптимізацію кількості інформаційних зв’язків
Стратегічна задача на оптимізацію кількості
інформаційних зв’язків між користувачами.
У деякій освітній системі є n працівників. Між деякими із них здійснюються двосторонні мобільні зв'язки.
Відомо, що з мобільного телефону будь-якого працівника можна додзвонитися до будь-якого мобільного іншого працівника.
Провайдер-фірма хоче вибрати декілька працівників і назвати їх вузловими операторами таким чином, що із будь-якого мобільного системи освіти існує прямий зв'язок до деякого вузлового оператора системи освіти.
Яку найменшу кількість вузлових міст треба обрати, щоб гарантовано, навіть у найгіршому випадку, вистачило усіх цих зв'язків провайдер-фірмі.
Відповідь: m(n)=n-[n/3]-1.
Вказівка. Переформулюємо умову задачі на мові теорії графів. Потрібно знайти таке мінімальне число s, що у будь-якому зв’язному графі, у якого n вершин можна відмітити не більше ніж s його вершин таким чином, що у будь-якої вершини знайдеться відмічена сусідня вершина(вважаємо, що сусідня вершина зветься сусідкою).
Доведемо, що s >= n-[n/3]-1. Розглянемо граф з чотирма вешинами v(0), v(1)j, v(2) j, v(3)j , j = 1, . . . , [n/3], та ребрами (v(0), v(1)j), (v(1), v(2)j), (v(2), v(3)j), j = 1, . . . , [n/3].
Нехай k - довільне число від 1 до [n/3]. У вершин v(2) k, v(3)k повинна бути відмічена сусідка, а це значить обов’язково буде відмічена v(2) k, як єдина сусідка v(3)k і одна з вершин v(1)j, v(3)j повинна бути відмічена, оскільки інших сусідів у v(2) k немає. Таким чином, всього повинно бути відмічено не менше 2*[n/3]-1 вершини.
Доведемо, що s <= n-[n/3]-1. Можна вважати, що заданий граф являється деревом, так як в протилежному випадку можна виділити скріплююче дерево і довести твердження для нього. Виберемо в якості кореня висячу вершину і назвемо її v(0),а інші розташуємо по рівнях стандартним чином. Розфарбуємо вершини в три кольори так, що вершини на рівнях 3k+1 пофарбовані в один колір, на рівнях виду 3k+2 пофарбовані в другий колір, а інші в третій колір. За принципом Діріхле знайдеться такий колір, в який пофарбовано що найменше [n/3]+1 вершини. Відмітимо вершини інших кольорів. Тоді ми відмітили не більше n-[n/3]-1 вершин, і у будь-якої невисячої вершини є відмічена сусідня вершина. Нехай v – висяча вершина(v не дорівнює v(0)), нехай v1 – батько– батько v1. ВІдмітимо, що v2 існує, так як рівнів не менше трьох. Якщо у v не існує відміченої v, v2 сусідньої вершини, то v1 – невідмічена, а значіть, відмічені v та v2. Приберемо мітку з вершини v, та відмітимо вершину v1. Тоді кількість відмічених вершин не зміниться, у всіх вершин, у яких була відмічена сусідка, вона залишається, а також вона і у вершини v тепер буде відмічена сусідка. Аналогічно зробимо для кореневої вершини. Зробивши, при необхідності подібну операцію скінчену кількість разів, ми отримаємо те, що у всіх вершин була відмічена сусідка. Що і вимагало довести.
вівторок, 19 грудня 2017 р.
Абстрактна функція Вінницького
Означення функції Вінницького.
Чи є такі властивості, які притаманні усім членам послідовності функцій:
…………….
g1(x)=f(x)/f’(x),
g2(x)=f2(x)/f’’(x),
……………
gт-1(x)=f n-1(x)/f (n-1)(x),
gn(x)=f n(x)/f (n)(x),
……………….,
якщо
f(x):R\{0}-->R\ {0};
f (n)(x): R\{0}-->R\{0};
Дослідження: Якщо розглянути безліч рівностей
….=g1(x)= g2(x)=……= gт-1(x)= gn(x)=…..
та виконати продовження послідовності вправо, то отримаємо:
1/f(x)=f(x)/f’(x) ,
тоді f2(x) = f’(x) ,
f (x) = (f’(x))0,5 .
Серед раціональних многочленів такої функції не має. Функцію f (x), що задовольняє рівність (*)
назвемо абстрактною функцією Вінницького.
Дайте відповідь на запитання:
Чи монотонна на області визначення абстрактна функція Вінницького?
Чи неперервна на області визначення абстрактна функція Вінницького?
Чи обмежена на області визначення абстрактна функція Вінницького?
Чи випукла на області визначення абстрактна функція Вінницького?
Дайте відповідь на запитання:
Чи монотонна на області визначення абстрактна функція Вінницького?
Чи неперервна на області визначення абстрактна функція Вінницького?
Чи обмежена на області визначення абстрактна функція Вінницького?
Чи випукла на області визначення абстрактна функція Вінницького?
субота, 9 грудня 2017 р.
Створення чарівних квадратів С. Вінницького
Вінницькі чарівні числові квадрати
Розташувати в клітинковому квадраті розміром (2k+1)x(2k+1), k єN, послідовні натуральні числа від 1 до (2k+1)2 так, щоб виконувалася умови:
1) Суми чисел із двох будь-яких двох клітинок, які симетричні відносно центральної клітинки, однакова. Тобто f+b=i+d=h+c=j+e=s+g=…=w+n.
w
|
z
|
u
|
t
|
s
|
q
|
h
|
f
|
e
|
r
|
x
|
i
|
а
|
d
|
p
|
y
|
j
|
b
|
c
|
o
|
g
|
k
|
l
|
m
|
n
|
2) Суми усіх чисел із клітинок, що утворюють квадратики, у яких центр симетрії співпадає з центром симетрії центральної клітинки, однакова. Тобто 2a=b+c+d+e+f+h+i+j= k+l+n+m+o+p+r+t+s+t+u+z+w+x+y+g. Сума чисел в зелених клітинках дорівнює сумі чисел в оранжевих клітинках і ці суми дорівнюють числу.
Розв’язання. Розглянемо спочатку квадрат 5х5.
Розглянемо набір із 12 найменших протилежних чисел та нуля. Тобто, випишемо їх в упорядку зростання:
-12; -11; -10; …. -3; -2; -1; 0; 1; 2; 3; …. 10; 11; 12.
Для цих чисел виконується властивість: сума двох протилежних дорівнює нулю. А якщо два протилежних числа розставляти в симетричних відносно центру квадрата клітинках, то сума їх рівні нулю. Розставляємо ці числа в даний квадрат 5х5.
ЧАРІВНИЙ КВАДРАТ 3х3 та 5х5
СЕРГІЯ ВІННИЦЬКОГО
| ||||
-9
|
-8
|
-7
|
-6
|
-5
|
-10
|
-2
|
3
|
1
|
12
|
-11
|
4
|
0
|
-4
|
11
|
-12
|
-1
|
-3
|
2
|
10
|
5
|
6
|
7
|
8
|
9
|
При такій розстановці чисел виконується умова, сума усіх чисел в зеленому квадраті дорівнює сумі усіх чисел в оранжевому квадраті.
До усіх чисел цього квадрату додамо число 13. Отримаємо:
ЧАРІВНИЙ КВАДРАТ 3х3 та 5х5
СЕРГІЯ ВІННИЦЬКОГО
| ||||
4
|
5
|
6
|
7
|
8
|
3
|
11
|
16
|
14
|
25
|
2
|
17
|
13
|
9
|
24
|
1
|
12
|
10
|
15
|
23
|
18
|
19
|
20
|
21
|
22
|
